How to Calculate Remainders of large numbers
November 13, 2013
Divisors of a Number – Sum and Product of Divisors
January 31, 2014http://youtu.be/Nj72Vw5voBM
Whats is Absolute value?
Absolute value (or Modulus) represented by |x| of a real number x is the non-negative value of x without regard to its sign.
For example:
Absolute value of -3 => |-3| = 3
Absolute value of 7 => |7| = 7
Absolute value as distance?
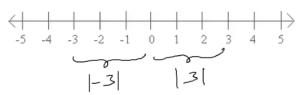
We can also think of absolute value of a number as its distance from zero. For example, consider this number line,
Here, the integer 3 is at a distance of 3 units from number 0. Similarly number -3 is also at distance of 3 units from 0. Since distance is always positive, we can say that,
The Distance of 3 from 0 => |3| = 3 &
The Distance of -3 from 0 => |-3| = 3
Now, if |x| = 3, then x is at a distance of 3 units from 0. From the number line, we get that the absolute of x = 3 or x = -3
In general, if |x| = a => x = a or x = -a. (Since x is at a distance of ‘a’ units from 0).
If |x| = a is the distance of x from 0, then what is |x-a|?
Distance of x from a number ‘a’ on the number line can be represented by |x-a|.
1. Solve the equation |x-2| = 3.
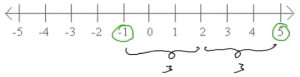
|x-2| = 3 implies x is at a distance of 3 units from 2. Representing this on the number line,
The numbers on the number line which are at a distance of 3 units from 2 are 5 and -1. Therefore, x = 5 or x = -1 are the values of the equation |x-2| = 3.
2. Solve the inequality |x-2| < 3
|x-2| = 3 implies x is at a distance less than 3 units from 2. Representing this on the number line,
From the number line, we see that all the points between -1 and 5 are at a distance less than 3 units from 2. Hence, the values taken by x is given by -1 < x < 5.
If you know what is |x| = a, can you explain what is meant by |x-a| + |x-b| ?
From our understanding of absolute value so far, we know that
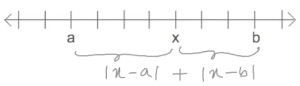
|x – a| represents the distance of x from a. Similarly |x – b| represents the distance of x from b. Implying that |x-a| + |x-b| is the sum of the distances of x from both a and b! :). This is evident from the number line,
Solve for x, |x+2| + |x-3| = 7
=> |x-(-2)| + |x-3| = 7
i.e we have to calculate the sum of the distances of x from -2 and 3.
Representing this on the number line,
![]()
From the image, we see that 4 is at distance of 1 unit from 3 and 6 units from -2. Hence, the sum of the distances of 4 from 3 and -2 is 7.
Similarly the sum of the distances of -3 from 4 and 3 is 7.
Therefore, x = 4 or x = -3 are the values of the equation |x+2| + |x-3| = 7.
When is the distance of x from ‘a’ and ‘b’ minimum?
We know that the sum of the distances of x from a and b is represented in terms of absolute value by |x – a| + |x – b|.
Now, |x – a| + |x – b| is minimum when x lies between a and b. The minimum value is given by |b-a|.
What is the minimum value of |x+2| + |x-3|?
=> Minimum value = |3-(-2)| = 5, which occurs for -2 ≤ x ≤ 3
Solving Absolute Value Equations
[section title=”Math Tricks Workout”]
Please do try our android app – Math Tricks Workout. The app is developed to improve mental arithmetic using a series of left to right fast math workouts.
Scan the QR code below or click on it for more details.
[/section]